Collatz Problemi Algoritmik Çözümü | Yazılım (C#)
Bir milyonun altındaki hangi başlangıç sayısı, en uzun zinciri üretir?
(NOT: zincir bir kere başladıktan sonra terimlerin 1 milyonun üzerine çıkabilmesi mümkündür.)
Zincir mi ne zinciri diyor olabilirsin senin için durumu daha açık bir hale getirelim hemen :)
Bir n sayısı
çift ise n= n/2
tek ise n= n*3 +1
bu mantıkla hareket ettiğimizde pozitif tam sayı olan her n sayısını teoride 1'e götürür.Buna Collatz Sanısı denir.Örneğin 9 sayısını başlatalım;
9 => 28 , 14 , 7 , 22 , 11 , 34 ,17 , 52 , 26 , 13 , 40 , 20 , 10 , 5 , 16 , 8 , 4 , 2 , 1
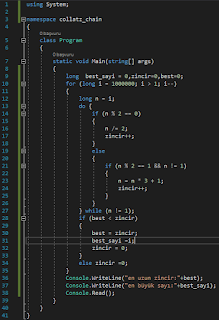
Toplamda 19 adımda ulaşıyor. O halde Sorumuza tekrar bir göz atalım ve buna göre algoritmamızı C# dilini kullanarak koda dökelim;
Cevap ise 837779 ve bu sayının oluşturduğu zincir ise 524 uzunluğunda :)
Kodlara şurdan ulaşabilirsiniz https://github.com/muhtesemozgur9/collatz_chain1/blob/master/Program.cs
(NOT: zincir bir kere başladıktan sonra terimlerin 1 milyonun üzerine çıkabilmesi mümkündür.)
Zincir mi ne zinciri diyor olabilirsin senin için durumu daha açık bir hale getirelim hemen :)
Bir n sayısı
çift ise n= n/2
tek ise n= n*3 +1
bu mantıkla hareket ettiğimizde pozitif tam sayı olan her n sayısını teoride 1'e götürür.Buna Collatz Sanısı denir.Örneğin 9 sayısını başlatalım;
9 => 28 , 14 , 7 , 22 , 11 , 34 ,17 , 52 , 26 , 13 , 40 , 20 , 10 , 5 , 16 , 8 , 4 , 2 , 1
Toplamda 19 adımda ulaşıyor. O halde Sorumuza tekrar bir göz atalım ve buna göre algoritmamızı C# dilini kullanarak koda dökelim;
Cevap ise 837779 ve bu sayının oluşturduğu zincir ise 524 uzunluğunda :)
Kodlara şurdan ulaşabilirsiniz https://github.com/muhtesemozgur9/collatz_chain1/blob/master/Program.cs


COLLATZ SANISI ÇÖZÜMSÜZ
YanıtlaSilGARİP AMA GERÇEK
Collatz sanısı: m = tek sayı ve x= sıfırdan büyük pozitif tam sayı(1,2,3,4,....k) olmak koşulu ile (2^x)*m)-1 şeklinde yazılan herhangi bir n tek sayısı için bir işlem (3n+1)/2 olarak alındığında, (2^x)*m)-1=n şeklinde yazılan bir sayı için (x) defa (3n+1)/2 şeklinde işlem yapılmak zorunda kalınır. Çünkü (x-1) defa işlem tek sayı çıkar. (x) inci ilem yapıldığında sayı çift sayı olur. Ama yinede bu hesap gözünüzü korkutmasın. İşlem sonucu (2^x)*m)-1=n şeklinde yazılan bir tek sayı (3n+1)/2 şeklinde x. inci işlem yapıldığında (3^x)*m)-1 olarak çift sayı olur. Bu kendi bulduğum formül sayesinde collatz sanısı için çözümün olmadığı bir sayının olabileceğini ispatlıyorum.
Collatz sanısı çözümsüz
ispat: test edeceğimiz tek sayıyı (2^x)*m)-1=n olacak halde yazdığımızda her tek sayı için uygulanan (3n+1)/2 işlemi ile ilk çift sayı (x) inci işlemin sonunda oluşur x= sonsuz olduğunda ise çözüm yoktur. Çünkü işlem sonsuz eksi bir defa tek sayı çıkacaktır. Sonsuzuncu işlem yapılsa idi, çift sayı çıkacak idi. ayrıca sonsuz eksi bir ifadesini veren sayı yoktur. Ama sonlu bir sayıyı ifade etmek amacı ile bu terim kullanılır.
Örnek verecek olursak:
(2^x)*m)-1=n denkleminde
x=3 ve m=7 olarak alacak olursak
(2^3)*7)-1 = n
(8)*7) -1= n
(56)-1=n olur
n=55olur
Normal hesaplama ile bu işlemi yaparsak işlemin x defa yapıldığını göreceksiniz. (x)=3 olduğuna göre 3 defa işlem yapacağız. yani kısaca (x) sayısı herhangi bir çift sayıyı tek sayı çıkana kadar ardarda iki ile böldüğümüzde kaç defa 2 ile bölüne bildiğini gösterir.
Biz test edeceğimiz tek sayıya 1 eklediğimizde sayı çift sayı olur. Bu çift sayıyı (2^x)*m ) haline getirip 1 çıkarırsak oluşan sayı yine bizim test yaptığımız tek sayı olur. Son hali ile test sayımız (2^x)*m)-1=n şeklinde olur. Şimdi örneğimizi bu halde yazalım.
55+1=56 Bu sayının kaç defa iki ile tam olarak bölündüğünü ve en son 2 ile bölümünden sonra çıkan tek sayıyı bulalım. Yani (x) ve (m) sayılarımızı bulalım. Test sayımız zaten belli, yani n=55
55+1=56 dan
1) 56/2=28
2) 28/2=14
3) 14/2=7
x=3 ve m=7
tek sayımız son hali ile (2^3)*7)-1=55 oldu tek sayı için uyguladığımız collatz işlemi (3n+1)/2 idi
1) işlem (55*3+1)/2=83
2) işlem (83*3+1)/2=125
3) işlem (125*3+1)/2=188
(x) Defa (3n+1)/2 şeklinde yapılan ardışık işlemlerin sonunda oluşan çift sayı (3^x)*m)-1 olacaktır.
Tek sayımız (2^x)*m)-1=n idi. Değerler yerine konulduğunda (2^3)*7)-1=55 şeklinde olur. Yine aynı şekilde değerleri ilk çift sayının kaç olduğunu bulmak için formülümüzde yerine koyarsak
(3^x)*m)-1 = (3^3)*7)-1 olur
(3^3)*7)-1= (27)*7)-1=188 sonuç bu şekilde de bulunur
Bu formül (2^x)*m)-1=n haline getirilmiş bütün tek sayılar için geçerlidir. Her tek sayı da bu halde yazılır zaten.
İrfan Aydoğan
doktor0906@hotmail.com